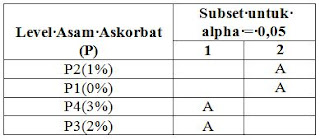
Kita memulai pada perlakuan dengan rerata
terbesar, yaitu P3 (2%), beri simbol “A” (anda bisa saja menggunakan simbol apa
saja) pada Subset 1. Nilai nyata terpendek (Rp) yang diperoleh di
atas unutk P3 = 5,615; selanjutnya tentukan semua nilai rata-rata yang sama
atau lebih besar dari nilai Rp P3 tidak berbeda nyata (0,05) dengan perlakuan
P3. Dari nilai rata-rata terlihat bahwa
P4 memiliki nilai rata-rata yang lebih besar dari nilai Rp P3 (6,25 vs 5,615), berarti bahwa P3
dan P4 tidak berbeda nyata (P>0,05). Beri simbol “A” untuk P4 pada Subset 1.
Deret nilai tengah mulai dari nilai terendah ke tinggi, diperoleh:
Tentukan nilai galat baku nilai tengah perlakuan dengan persamaan dibawah:
Selanjutnya, tentukan nilai nyata terpendek Duncan:
Dari nilai nyata terpendek Duncan diatas selanjutnya tentukan nilai wilayah nyata terpendek berdasarkan pengurangan nilai
tengah dengan nilai nyata terpendek Rp untuk nilai wilayah terpendek 5% dan 1%:
Menentukan
perbedaan pada taraf 5%: Buatlah
tabel dengan dua kolom subset untuk mengelompokkan perlakuan-perlakuan yang
tidak menunjukkan perbedaan yang signifikan, seperti pada contoh dibawah. Kolom
subset sebanyak dua buah merupakan jumlah subset minimum, karena hasil ANOVA
yang signifikan berarti bahwa terdapat minimal sebuah perlakuan yang berbeda
dengan perlakuan lainnya. Selanjutnya kelompokkan perlakuan berdasarkan subsetnya masing-masing.
Kita memulai pada perlakuan dengan rerata terbesar, yaitu P3 (2%), beri
simbol “A” (anda bisa saja menggunakan simbol apa saja) pada Subset 1. Nilai nyata terpendek (Rp) yang diperoleh di
atas unutk P3 = 5,615; selanjutnya tentukan semua nilai rata-rata yang sama
atau lebih besar dari nilai Rp P3 tidak berbeda nyata (0,05) dengan perlakuan
P3. Dari nilai rata-rata terlihat bahwa
P4 memiliki nilai rata-rata yang lebih besar dari nilai Rp P3 (6,25 vs 5,615),
berarti bahwa P3 dan P4 tidak berbeda nyata (P>0,05). Beri simbol “A” untuk
P4 pada Subset 1.
Selanjutnya perhatikan
perlakuan dengan rerata besar ke-2, yaitu P4. Tentukan semua nilai rata-rata
yang sama atau lebih besar dari nilai Rp P4= 5,560 tidak berbeda nyata (0,05) dengan perlakuan
P4. Dari semua nilai rata-rata yang
lebih rendah dari nilai rata-rata P4, memiliki nilai rata-rata yang lebih kecil
dari nilai Rp P4 (5,41 vs 5,56) dan (5,36 vs 5,56), berarti bahwa antara P4 dengan P1 dan P2
berbeda nyata (P<0,05). Beri simbol “A” untuk P1 dan P2 pada Subset 2.
Selanjutnya kita akan
membandingkan dua perlakuan terakhir yaitu antara P1 dan P2. Nilai Rp P1= 4,752. Nila
rata-rata P2= 5,36 lebih besar dibandingkan dengan nilai Rp P1 (5,36 vs 4,752), yang berarti bahwa tidak terdapat perbedaan
yang nyata (p>0,05) antara P1 dan P2.
Dengan demikian, tidak ada lagi penambahan subset (atau hanya terdapat
dua subset), “andai kata” pada pembandingan antara P1 dan P2 terdapat beda yang
nyata, maka akan bertambah satu subset baru, sehingga tabel di atas akan berubah
menjadi berikut:
Kelanjutan analisis di atas
unutk tingkat ketelitian alpha=0,01, silahkan digunakan untuk latihan.
KEPUTUSAN
Analisis Variannsi: Fhitung (5,07) lebih besar dari Ftabel 1% (4,06), maka perlakuan
pemeriana asam askorbat terhadap dangke berpengaruh secara nyata (P<0,01)
terhadap nilai TBA dangke yang disimpan selama 7 hari;
Uji Beda Nyata Terkecil (Uji-BNT) :Sampel yang memperoleh perlakuan Asam Askorbat 2% memiliki nilai
TBA yang secara nyata lebih tingi (P<0,05) dibandingkan dengan nilai TBA
sampel yang diberi Asam Askorbat 0% dan 1%, namun tidak berbeda (>0,05)
dibandingkan dengan sampel yang diberi Asam Askorbat 3%;
Analisis dengan SPSS dapat dilihat pada Link Berikut: <...tahap pembuatan...>
by: Mawardi A. Asja (InsyaAllah bermanfaat)